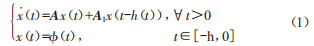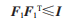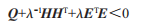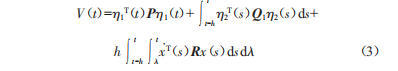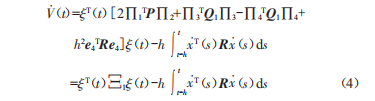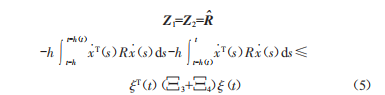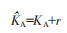引言
電力系統(tǒng)是一個(gè)分布地域較廣、元件眾多、動(dòng)態(tài)響應(yīng)速度快的大規(guī)模系統(tǒng),某一元件的擾動(dòng)可能很快波及全系統(tǒng):它本質(zhì)上也屬?gòu)?fù)雜的非線性動(dòng)力系統(tǒng),在運(yùn)行過(guò)程中經(jīng)常可能受到各種自然及人為的擾動(dòng)。分析電力系統(tǒng)在不同等級(jí)擾動(dòng)下的暫態(tài)和動(dòng)態(tài)行為,同時(shí)以此為基礎(chǔ)提出并及時(shí)采取針對(duì)性的控制措施,是電力系統(tǒng)設(shè)計(jì)與運(yùn)行最為重要的任務(wù)。廣域測(cè)量系統(tǒng)的使用能夠有效地為分析和控制復(fù)雜大電網(wǎng)提供系統(tǒng)信息,如何對(duì)廣域信息進(jìn)行有效的監(jiān)測(cè)及利用,提升系統(tǒng)分析結(jié)果的準(zhǔn)確性和有效性,改善針對(duì)擾動(dòng)的控制過(guò)程和效果,是我們不斷努力的方向。在傳輸中,廣域信號(hào)可能會(huì)出現(xiàn)一定程度的通信時(shí)滯,而且對(duì)廣域電力系統(tǒng)也可能會(huì)帶來(lái)影響,使其最終成為時(shí)滯電力系統(tǒng)。所以,從電力系統(tǒng)穩(wěn)定性方面來(lái)看時(shí)滯性的研究具有重要作用,可確保廣域電力系統(tǒng)的穩(wěn)定運(yùn)行。
眾所周知,在對(duì)電力系統(tǒng)時(shí)滯穩(wěn)定性進(jìn)行研究時(shí)最常用的方法有兩種:頻域分析法、時(shí)域分析法。若系統(tǒng)出現(xiàn)不確定性或時(shí)變時(shí)滯,很難找到解決方法,這是頻域法的局限性。而時(shí)域法在處理含有不確定項(xiàng)、參數(shù)變動(dòng)和時(shí)變時(shí)滯系統(tǒng)時(shí)優(yōu)勢(shì)明顯,也正因此如今在對(duì)電力系統(tǒng)時(shí)滯穩(wěn)定性探索時(shí)較為注重這種方法。而用Lyapunov泛函結(jié)合積分不等式的方法,能夠有效研究電力系統(tǒng)。文獻(xiàn)是通過(guò)引入一些必要的自由權(quán)矩陣,限制了導(dǎo)數(shù)以及時(shí)變時(shí)滯可微性,使系統(tǒng)的保守性無(wú)形中被降低。文獻(xiàn)是以狀態(tài)軌跡定義為主對(duì)狀態(tài)變量進(jìn)行定義,最終確定為線性函數(shù)與對(duì)線性部分的偏離函數(shù)之和,然后結(jié)合"時(shí)滯分割",獲得系統(tǒng)穩(wěn)定性判據(jù)。文獻(xiàn)中由一組線性矩陣不等式表示導(dǎo)函數(shù),而在對(duì)泛函導(dǎo)數(shù)進(jìn)行推導(dǎo)的過(guò)程中,可以引入松散項(xiàng)使判據(jù)所具有的保守性有效降低。
基于以上分析,本文建立了全新的Lyapunov-Krasovskii泛函,進(jìn)行電力系統(tǒng)魯棒穩(wěn)定性分析,避免了對(duì)時(shí)變時(shí)滯可微的限制,引入逆凸不等式以及增廣的Lyapunov-Krasovskii泛函各一個(gè),求得新的穩(wěn)定性判據(jù)。且使用仿真算例進(jìn)行了驗(yàn)證,最終得出該判據(jù)相較于現(xiàn)有的一些成果,減少保守性的效果更好。
本文標(biāo)號(hào)如下:Rnxm、Rn分別表示實(shí)數(shù)域的n×m階矩陣空間與n維向量空間:上標(biāo)H-1和HT分別代表矩陣的逆與轉(zhuǎn)置:"*"代表對(duì)稱(chēng)矩陣的對(duì)稱(chēng)項(xiàng):I和О分別代表合適維度的單位矩陣和零矩陣:同時(shí)sym(X)=X+XT:P>0意味著矩陣P是對(duì)稱(chēng)與正定的。
1系統(tǒng)描述
考慮如下時(shí)變時(shí)滯線性系統(tǒng):
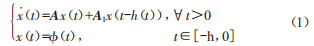
式中,x(l)∈Rn是系統(tǒng)狀態(tài)向量:初始條件6(l)為連續(xù)可微的向量函數(shù):A,A1∈Rn是恒定系統(tǒng)的矩陣:h(l)是時(shí)變時(shí)滯且滿足0<h(l)<h。
電力系統(tǒng)在實(shí)際情況下是存在擾動(dòng)的,所以上述模型并不能反映實(shí)際的電力系統(tǒng)工作狀態(tài),以下是含有不確定性的
系統(tǒng)模型:
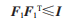
假設(shè)[AAAA1]=CF1[EaEb]為系統(tǒng)擾動(dòng)項(xiàng),C、Ea、Eb是已知的合適維數(shù)的常數(shù)矩陣,F1是變化矩陣,滿足條件:
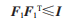
引理1[7]:對(duì)任意正定矩陣T∈Rn×n,常數(shù)a、b,向量函數(shù)x在區(qū)間[a,c]二Rn,有:

引理3:給定具有合適維數(shù)的矩陣Ω=ΩT、H、E,并且Ω+HF(l)E+ETFT(l)HT.0,對(duì)所有滿足F(l)FT(l)≤I的F(l)都成立的充分必要條件是存在一正數(shù)A<0,使得下式成立:
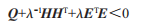
2時(shí)滯電力系統(tǒng)穩(wěn)定性判據(jù)


證明:
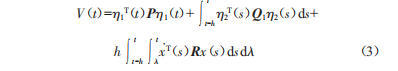
當(dāng)P>0、01>0、R>0時(shí),該函數(shù)正定,即v(t)>0,求導(dǎo)可得:
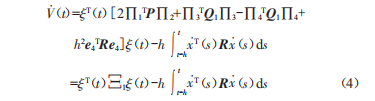
式中積分項(xiàng)可以改寫(xiě)成以下形式:

由引理1可知:

由引理2可知:
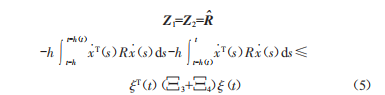
加入一個(gè)自由權(quán)矩陣,下列等式成立:

從引理3可知,當(dāng)λ>0時(shí)能夠得出:
1+2+3+4+A-191T91+A92T92<0
因此v'(t)<0,由此可得系統(tǒng)(2)是漸進(jìn)穩(wěn)定的,證明完畢。
3算例分析
通過(guò)使用單機(jī)無(wú)窮大系統(tǒng)得出圖1。
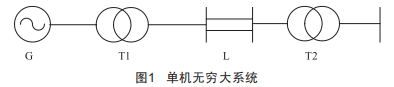
假設(shè)系統(tǒng)存在單一時(shí)滯時(shí)對(duì)應(yīng)的矩陣參數(shù)如下:

如果勵(lì)磁放大系數(shù)會(huì)根據(jù)情況有一定的擾動(dòng),則擾動(dòng)影響后的實(shí)際系數(shù)為:
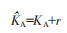
式中,就勵(lì)磁放大系數(shù)而言KA為整數(shù)值,r為標(biāo)量,能夠表示勵(lì)磁放大系數(shù)擾動(dòng)情況,在研究r影響系統(tǒng)穩(wěn)定性情況時(shí),矩陣C、Ea、Eb的取值為:

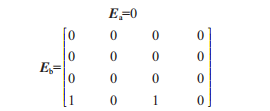
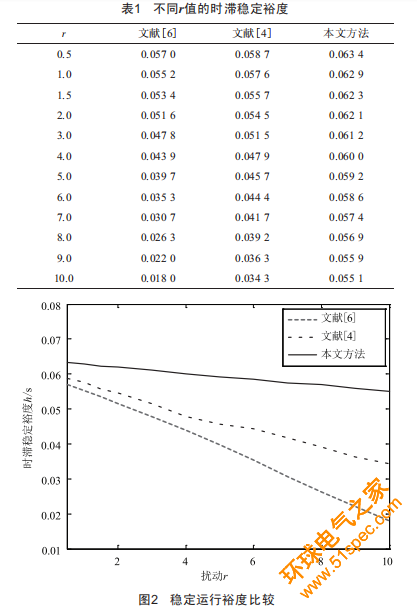
根據(jù)本文的定理,求出不同勵(lì)磁擾動(dòng)在r滿足約束條件0<h(t)<h時(shí),系統(tǒng)的穩(wěn)定裕度隨r的增大而減小,并與文獻(xiàn)的數(shù)值進(jìn)行了對(duì)比,如表l和圖2所示,從而體現(xiàn)出了本文方法的可行性。
4結(jié)語(yǔ)
本文針對(duì)時(shí)變時(shí)滯對(duì)單機(jī)無(wú)窮大系統(tǒng)穩(wěn)定性的影響,構(gòu)造全新的Lyapunov-Krasovskii泛函,就積分項(xiàng)求解過(guò)程而言,使用文獻(xiàn)[8]所述方法處理,其中還加入了自由權(quán)矩陣,得出了時(shí)變時(shí)滯穩(wěn)定的新判據(jù)。通過(guò)數(shù)值對(duì)比,可以看出本文方法在減小保守性方面的效果更好。